今回は、「指数の基本的な計算」についての説明です。
1.初めに
指数には、基本的な法則・指数法則というものが存在します。
今回は、どんな指数法則があるのか、何故その関係が成り立っているのかなどを順番に解説していこうと思います。
『指数とか“e”って何?』という状態の方は先に以下の記事に目を通してください。

2.指数が自然数の時の指数法則
まずは、指数が自然数(ここでは0を含まない正の整数と定義)である時の指数法則について触れていきます。
最も基本的な法則です。
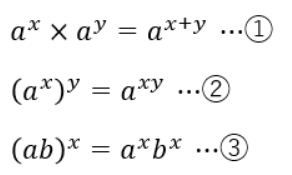
実際に計算してみればこの通りになるので、順番に見ていきましょう。
【①式の確認】
底が揃っているべき乗同士の掛け算は、指数を足して表現できるという法則です。
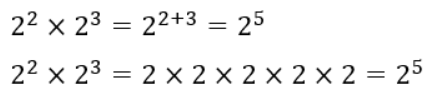
ちなみに、掛け算が成り立っているので、割り算も成り立ちます。
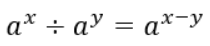
【②式の確認】
べき乗をべき乗にすると、指数を掛け合わせたものに等しくなるという法則です。
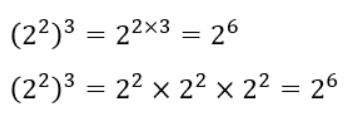
【③式の確認】
掛け算をべき乗にすると、数字をそれぞれべき乗にした上で掛け合わせたものと等しくなるという法則です。
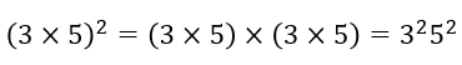
上記の式が最も基本的な法則です。どれもよくよく考えれば当然の結果ですけどね。
3.指数が整数の時の指数法則
次は、指数が自然数以外…0や負の整数である時も①~③の法則が成り立つと仮定した場合に見えてくる法則についてです。
①式にx=1、y=0を代入すると、以下のようになります。
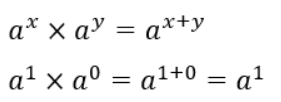
ここで両辺を見比べると、a0=1になることがわかります。
次は、①式にx=n、y=-nを代入してみます。
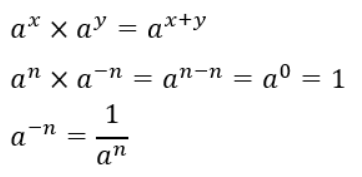
すると、指数が負の整数になった場合の法則が導き出されます。
なので、指数が0や負の整数である時も①~③の法則が成り立つと仮定した場合、以下の式が成り立つことになります。
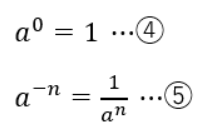
※aは0以外、nは正の整数という条件下に限る。
逆に言うと、④⑤式さえ成り立っていれば、指数が0や負の整数になっていても①~③の法則は成り立つと言えます。
そこで、④⑤式が成り立つものと定義することで、指数法則が整数の時に成り立つものとしているわけです。
要するに、④⑤式の存在は都合が良いように定義してあるだけなんですよ。
⑤式に関しては指数がマイナスになるマイナス乗が登場するので、理解しづらいかと思います。
なので、少し補足します。
20を起点として順番に2を掛けていくと、以下のようになりますよね?
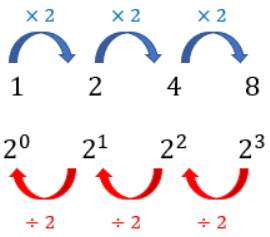
この関係なら理解できるはずです。
2を1回掛ければ指数が1増え、2で1回割れば指数が1減るだけですから。
では、20を起点として、順番に2で割っていくとどうなりますか?
2で1回割ると指数が1減ってくんですよね?
答えは、以下の図のようになります。
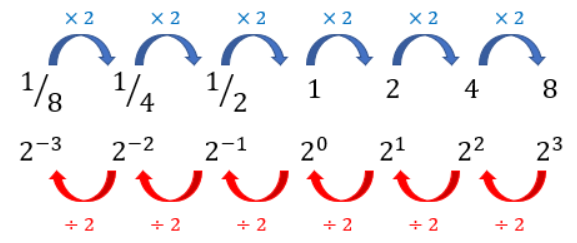
つまり、指数がプラスの時は底を1に何回掛けているかを表していて、マイナスの時は底を1から何回割っているかを表しているんです。
マイナス乗と考えるからわかりづらいだけで、本質的には大したことをしていないんですよ。
以上、「指数の基本的な計算」についての説明でした。



