今回は、「逆関数の微分」についての説明です。
1.逆関数の微分
f(x)に対してg(y)という逆関数が存在しているとします。
y=f(x)に対してx=g(y)が成り立っている関係ですね。
逆関数については以下の記事にまとめてあるので、知らないという方はまずはそちらから参照してください。
y=f(x)とx=g(y)の微分はそれぞれ以下のような関係を持っています。
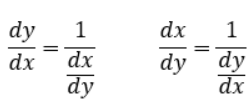
つまり、逆関数の微分は、逆関数の逆関数(元の関数であるf(x)が該当)を微分した値の逆数になるわけです。
元の関数の微分が逆関数の逆数とも言えますね。
なんか混乱してきますね…。
この関係を知っていると、場合によっては微分が簡単に行えるようになります。
例を見てみましょう。

まあ、逆関数を使わなくても普通に計算可能ですが、こんな導き方もあるんだと頭の片隅にでも置いておきましょう。
2.関係式の導き方
覚える必要があるかは微妙なところですが、どうやってその関係式を導き出しているのかを記述していきます。
f(x)という関数を微分する場合の定義は以下のようになっていました。
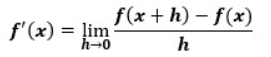
この定義に則ると、逆関数g(y)の場合は以下のようになります。

まず、逆関数の定義式の関係を図で表すと、以下のようになります。
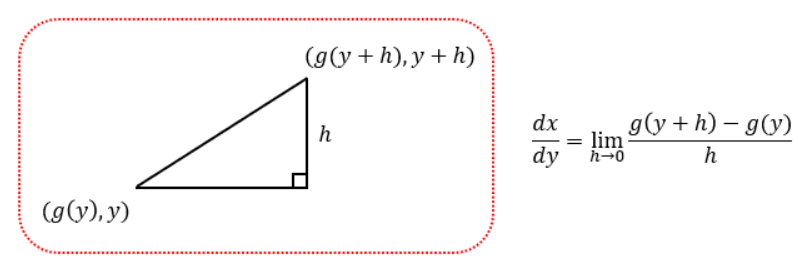
これに対して、逆関数になる前の関数は、以下のように表せます。
※逆関数でhを使用しているので、差をjと置いている。
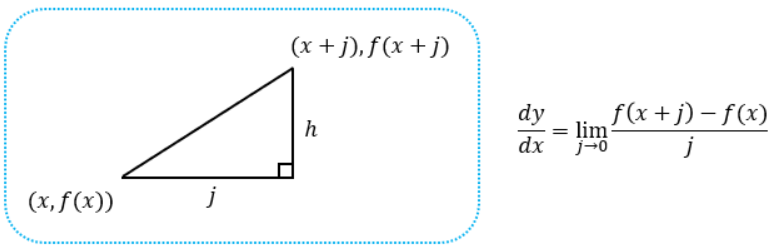
これらの関係から、以下の関係が成り立っていることがわかります。
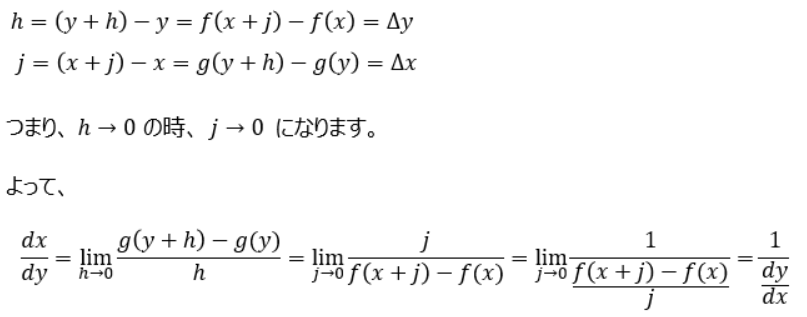
これで関係式を導き出すことができました。
以上、「逆関数の微分」についての説明でした。





