今回は、「微分の定義と実際の解き方」についての説明です。
1.微分の定義とlimitの意味
微分は正式には以下のように定義されています。
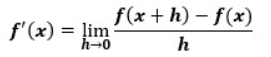
xに関する関数のことをf(x)と表示する為、f(x+h)も関数です。
平たく言えば、2xやx2+1のようなxを含む数式がf(x)ということです。
それに対し、f(x+h)はf(x)の”x”に”x+h”を代入したものとなります。
f(x)=2xだったとすると、f(x+h)=2(x+h)になる…といった感じです。
そして、f(x)を微分した結果をf'(x)のように表示します。
定義のlimというのは前回のそもそも微分とは何なのかを説明した記事でもしれっと出てきました。
一応説明をすると、“lim”とは“limit”のことです。
[limit]は[限界]という意味です。
では何が限界なのかと言うと、limの下に書かれている条件を限界まで実行してほしいのです。
つまり、定義式の場合は「次に続く関数の内、変数hを限りなく“0”に近づけてください」という意味になります。
なので、f(x+h)とf(x)という関数に含まれるh及び分母のhに“0”を代入するとf'(x)が求まることになります。
まあ、微分=傾きという関係性さえ理解できているならこの定義式の形は覚える必要ないですけどね。
ちなみに、xに関する関数はyで表してあることもある為、f(x)=2xという式があった場合はf(x)=y=2xだと思ってもらって問題ないです。
2.微分して得られた関数を表現する記号
定義の説明でちょこっと出ていますが、微分して得られた関数を表す記号があります。
f'(x)というヤツです。
この「'(シングルクォーテーション)」が付いていると微分されたことを意味しています。
なので、y’なども微分を表しているわけですね。
読み方は「y'(ワイダッシュ)」のように「ダッシュ」と読むのが一般的です。
「プライム」とも呼ぶようですが、個人的にそう呼んだことは無いです。
この微分して得られる関数のことを導関数と呼びます。
なので、『導関数を求めよ』という問題があったとすると、『微分せよ』と同じ意味合いを持つということになります。
3.導関数と微分係数の違い
導関数と似た用語に微分係数というものがあります。
意味は確かに似ているのですが、指してる範囲が全く違うので説明していきますね。
導関数は、f(x)という関数のあらゆる点における傾き(微分結果)を得ることができる関数のことです。
以下のような二次関数があったとして、点Aでも点Bでも点Cでも…どこの点での傾きも得られる数式が導関数なのです。
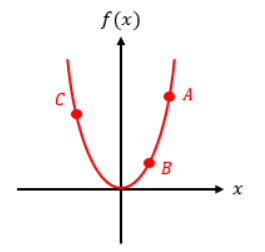
傾きを求めたい点のx軸座標を代入すれば、傾きを求めることが可能です。
それに対して、ある特定の一点における傾きを指しているのが微分係数です。
点Aか点Bか点Cか…どれか一点の傾きのことを指しているんですね。
つまり、導関数の中に微分係数が含まれているのです。
よく混同されている方がいるので注意しましょう。
まあ、関数と係数の違いを理解していればイメージはできるんですけどね。
4.微分を表現する記号
f(x)を微分すればf'(x)になるのはわかったと思います。
次は微分自体を表現する記号についてです。
微分を表現する記号はd/dxと書きます。
読み方は普通に「ディーディーエックス」と読みます。
高校数学ではdy/dx(ディーワイディーエックス)という形で見たことがあるのではないでしょうか?
あれは、「yという関数のxについて微分してください」という意味です。
あくまで微分を表すのはd/dxの部分です。
仮にdy/dtとなっていた場合、「yという関数のtについて微分してください」という意味になります。
分母の文字によって微分する対象が変化することに注意しましょう。
詳しくは例を用いて次項から説明します。
ちなみに、dは微分を意味する[differential]のdです。
5.高校数学における微分の計算方法
高校数学ではどこかしらに微分の定義式が(多分)載っていましたが、実際に計算する際に毎回定義に則って計算した記憶はないかと思います。
X2を微分すると2xになるといった公式・考え方があったはずです。
ということで、以下の式が微分の基本公式です。
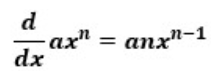
公式を見ると頭が痛くなる方もいるかと思いますので、実際に問題を解いてみて感覚で覚えましょう。
ポイントさえ押さえておけばあまり難しく考える必要はありません。
柔軟に考えましょうね。

補足説明をしますね。
例1
基本公式に則っただけなので特に無し。
公式と見比べてどう計算したのかまず理解しましょう。
例2
xを含む数式が複数個ある場合、個別にd/dxがかかります。
分割して基本方式を当て嵌めてください。
例3
xを含まない定数(1や2などの数字)はx0がくっついているのと同じに考えることができるので、微分すると0になる。
例4
xについて微分しているので、x以外の変数(ここではt)に関しては定数扱いする。
例5
xについて微分しているので、t2は定数扱いで変化しません。
例6
マイナス乗になっても考え方は変わりません。
この辺りを押さえておけば学校で習うレベルの微分なら大体解けます。
一部特殊なものを除けばね。
以上、「微分の定義と実際の解き方」についての説明でした。




