【基礎から学ぶ三角関数】 二倍角の公式とは？ ～sin2αなどの解法～

今回は、「二倍角の公式」についての説明です。

１．二倍角の公式とは？

三角関数の二倍角の公式とは、sin2αのように角度が二倍になっている場合の公式を指します。

公式の名前通りですね。

公式は以下のようになっています。

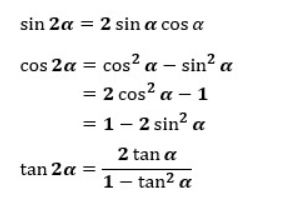
次項から公式の証明をしていきますが、加法定理を使うだけで簡単に求めることができます。

２．sin2αの証明

まずはsin2αの証明から始めます。

2αを(α+α)とみなして加法定理を適用するだけですけどね。

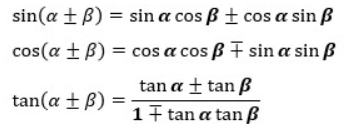
sin2α=sin(α+α)=sinαcosα+cosαsinα=2sinαcosα

はい、証明終了です。
簡単ですね。

３．cos2αの証明

次はcos2αの証明です。

sin2αと同じように計算してみましょう。

cos2α=cos(α+α)=cosαcosα－sinαsinα=cos²α－sin²α

sin²α+cos²α=1なので、式を変形したsin²α=1－cos²αまたはcos²α=1－sin²αを代入すると、

cos²α－sin²α=1－2sin²α=2cos²α－1になります。

４．tan2αの証明

最後にtan2αの証明です。

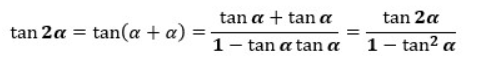
以上です。

二倍角の公式に関しては複雑そうに見える割には単純です。
最悪求め方さえ覚えておけばすぐに計算が可能なので、覚えておく必要が無い筆頭だったり…。

ちなみに、同じ要領で三倍角・四倍角と求めていくことが可能です。
使うかどうかは置いといてね。

以上、「二倍角の公式」についての説明でした。

---