今回は、「sinθの2乗の2の付く位置」についての説明です。
1.sinθの2乗の表記
三角関数の公式でsin2θ+cos2θ=1という関係式を見たことがありませんか?
高校で義務教育を受けていれば教科書に載っていたのではないかと思います。
昔から疑問だったのですが、そもそもsin2θって何を指しているのでしょうね?
sinを2乗しているのか、sinθを2乗しているのか…θを2乗しているわけではないのは確かですけどね。
答えは、sinθを2乗しているようです。
数学の一般的な記法に従うならば、本来は sin2θ=sin(sinθ)のはずなのですが、何故だか三角関数の場合だけsin2θ=(sinθ)2という意味になるようです。
不思議ですね。
これに関してはそういうものだと覚えるしかないので、何度も見直して頭にインプットしましょう。
2.sin2θ+cos2θ=1の導き方
三角関数には様々な公式・定理が存在しますが、その中でも有名な公式としてsin2θ+cos2θ=1という関係式があります。
メジャーな公式なので覚えている方は比較的多いかと思いますが、何故そうなるかを考えたことがある方は少ないと思います。
なので、ここではこの関係式を導いてみようと思います。
「三角関数と正弦曲線の関係」の説明で単位円の座標について考えていました。
この関係を考えている時、原点から角度θ方向にある単位円上の座標は(cosθ,sinθ)と表せることがわかっています。
ということは、原点と点Aを結んだ線を斜辺とした直角三角形を描いた時、各辺は横辺cosθ、縦辺sinθ、斜辺1の関係になります。
なので、三平方の定理よりsin2θ+cos2θ=1が成り立つことがわかります。
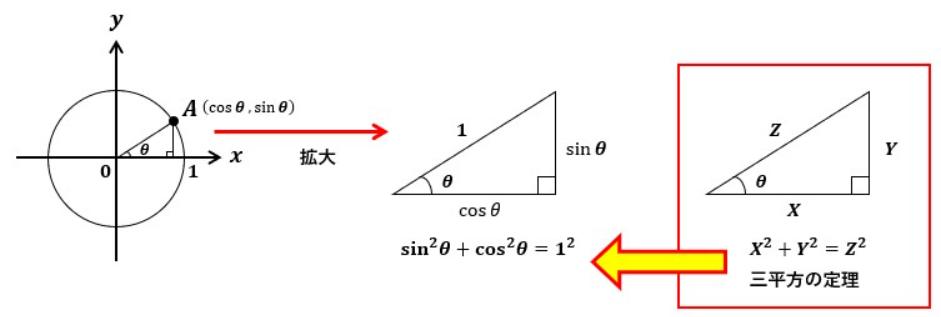
もしくは、三平方の定理から以下のように逆算することも可能です。
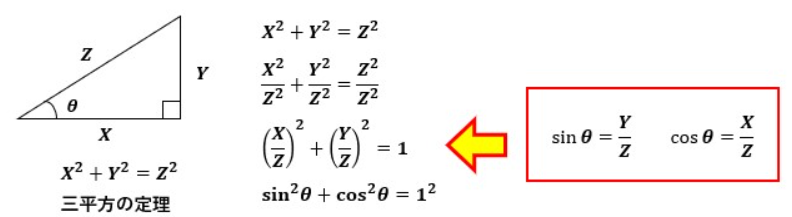
数学は公式を覚えていなくても最悪計算すればわかったりするのがいいですねー。
以上、「sinθの2乗の2の付く位置」についての説明でした。




