今回は、「三角関数の基礎であるsin・cos・tan」についての説明です。
1.三角関数とは?
sin(サイン)・cos(コサイン)・tan(タンジェント)という言葉をどこかで耳にしたことはありませんか?
sin・cos・tanのことを三角関数と呼びます。
sin・cos・tanは高校数学で習う内容で、直角三角形の三つの辺の内、ある角度の時の二つの辺の長さの比を表したものを指します。
三角形は内角の和が180°になります。
直角三角形に関しては一つの角は90°固定なので、直角三角形の一つの鋭角の角度(x°)がわかると残るもう片方の鋭角の角度(90°-x°)もわかります。
直角三角形の場合、この鋭角の角度によって辺の比が決定するようにできています。
つまり、直角三角形の角の大きさと辺の長さの比は関数になっていて、その関数がsin・cos・tanなのです。
(直角)三角形の関数だから三角関数という単純な命名です。
ある角度の時の直角三角形の二辺の比を表す関数なので、三角比とも呼ばれます。
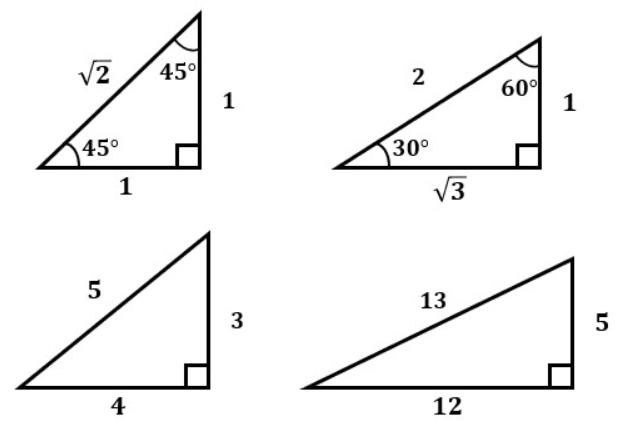
「三平方の定理」の説明でも述べているのですが、有名どころでは以下のようなパターンがあります。
一つの鋭角が30°、45°、60°になっている場合はよく出てくるので、覚えておきましょう。
2.sinの表し方
まずはsinの表し方から説明していきます。
sin・cos・tanは“直角三角形の三つの辺の内、ある角度の時の二つの辺の長さの比を表したもの”と述べました。
図2のような直角三角形がある場合、角度θの時のsinはAC/ABと表します。
つまり、辺ABと辺ACの比を表すのがsinです。
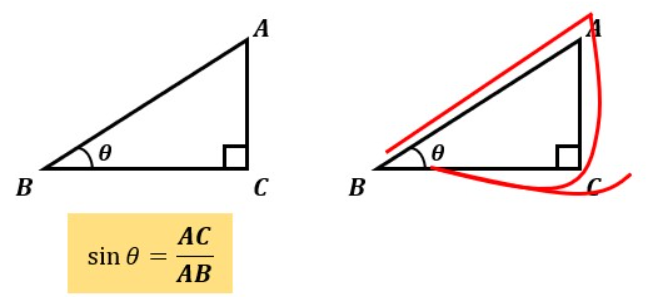
覚え方ですが、筆記体の“s”の描き順で直角三角形をなぞってください。
すると、辺ABを通った後に辺ACを通りますよね?
最初に通った辺を分母、次に通った辺を分子に当て嵌めてみてください。
それがsinθになります。
つまり、sinは直角三角形の直角を右下に位置させた状態で鋭角θを基準とした時の斜辺と縦辺の比を表しています。
“直角三角形の直角を右下に位置させる”のが基本なので、この機に覚えておいてください。
3.cosの表し方
次はcosです。
図3のような直角三角形がある場合、角度θの時のcosはBC/ABと表します。
つまり、辺ABと辺BCの比を表すのがcosです。
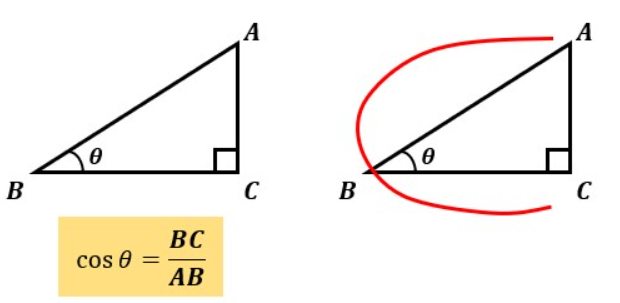
覚え方ですが、筆記体の“c”の描き順で直角三角形をなぞってください。
すると、辺ABを通った後に辺ACを通りますよね?
最初に通った辺を分母、次に通った辺を分子に当て嵌めてみてください。
それがcosθになります。
つまり、cosは直角三角形の直角を右下に位置させた状態で鋭角θを基準とした時の斜辺と横辺の比を表しています。
4.tanの表し方
最後はtanです。
ここまでの流れからどうなるかは予想つくんじゃないですかね?
そうなるように書いているわけですが。
図4のような直角三角形がある場合、角度θの時のtanはAC/BCと表します。
つまり、辺BCと辺ACの比を表すのがtanです。
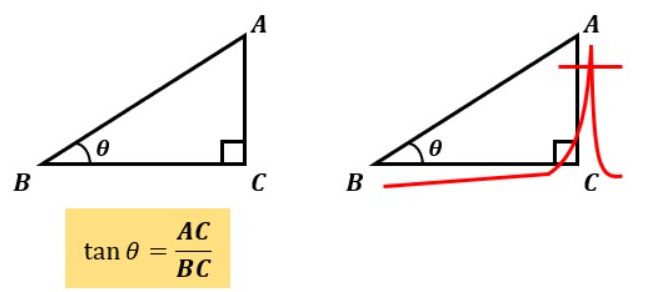
覚え方ですが、筆記体の”t”の描き順で直角三角形をなぞってください。
すると、辺BCを通った後に辺ACを通りますよね?
最初に通った辺を分母、次に通った辺を分子に当て嵌めてみてください。
それがtanθになります。
つまり、tanは直角三角形の直角を右下に位置させた状態で鋭角θを基準とした時の横辺と縦辺の比を表しています。
以上のように、sin・cos・tanは同じルールで定義されているので、一度覚えてしまえばそう簡単に忘れることはなくなります。
5.まとめ
長ったらしい説明をしたので、内容を簡単にまとめておきます。
例えば、sinθ=4/5になっていたとします。
sinθ=4/5という関数が表すのは、直角三角形において角度θの鋭角を基準にすると斜辺:縦辺=5:4に必ずなるということです。
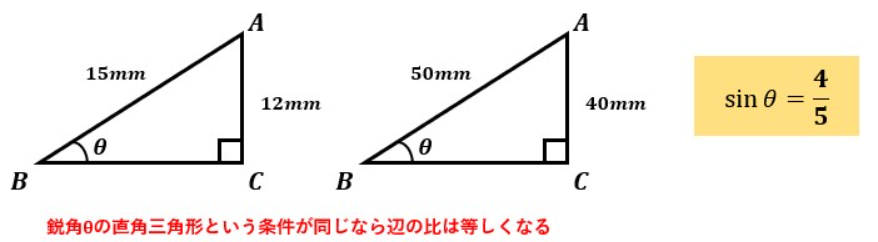
cosとtanに関しても同様です。
結局のところ、鋭角θを持つ直角三角形という条件が揃っている場合の辺の比を表しているのがsin・cos・tanというだけです。
あまり難しく考えないようにしましょうね。
以上、「三角関数の基礎であるsin・cos・tan」についての説明でした。




