今回は、「CMOS論理回路」についての説明です。
1.CMOS論理回路の組み合わせ
NOT回路・NAND回路・NOR回路をCMOS論理回路で表す方法は以下の記事で述べました。

今回は、これらのCMOS回路を組み合わせた回路を見ていこうと思います。
2.例題①
図1の論理式はどうなるか考えていきましょう。
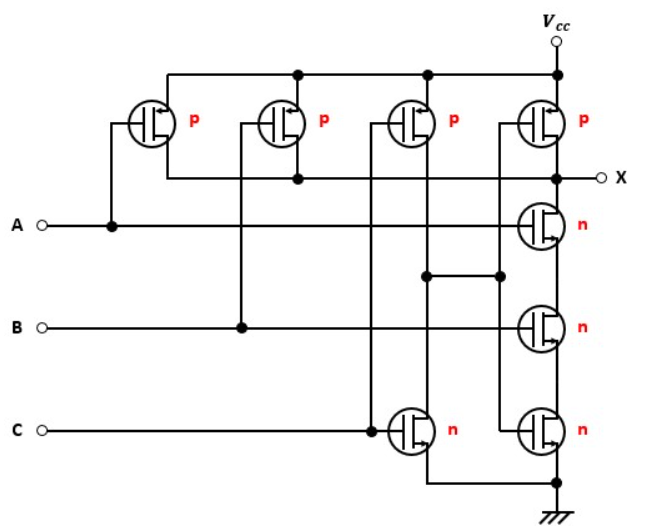
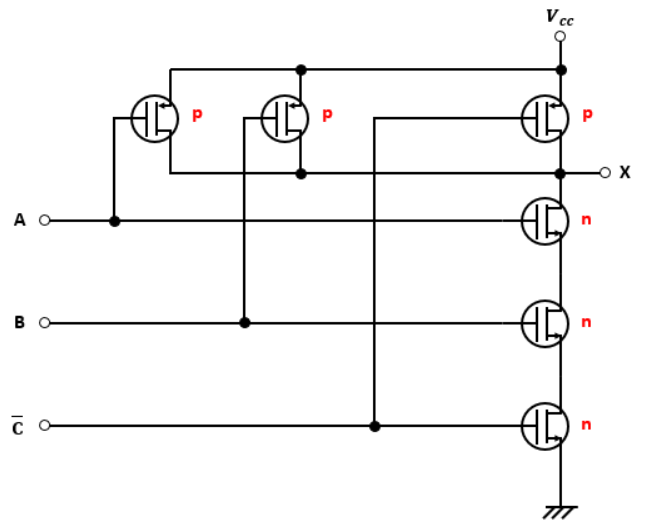
まず注目すべきは一番右の列です。
p型MOSFETが1つに対してn型MOSFETが複数ありますよね?
なので、最終的にはNAND回路になっていることがわかります。
これに関してはCMOS論理回路のNAND回路とNOR回路をよく見てればわかります。
問題は出力Xに入ってくる論理変数です。
このままでは何が何やら意味がわからないかと思います。
なので、分解して考えてみましょう。
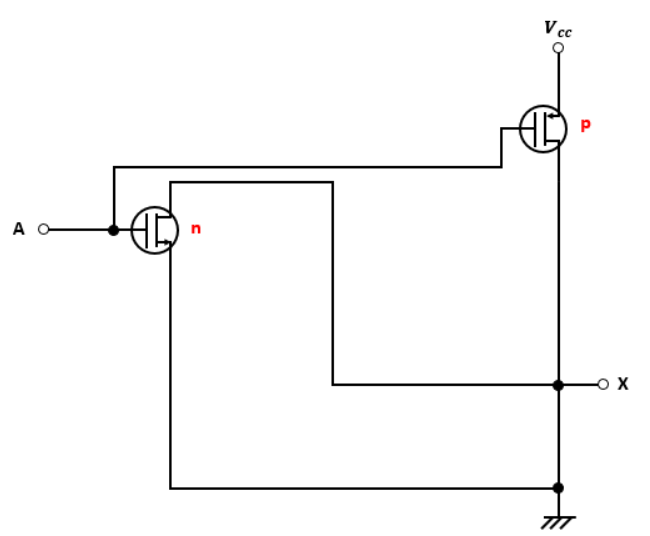
まずは図2のように抜き出してみました。
ここだけ見るとただのNOT回路なので、出力XはAになります。
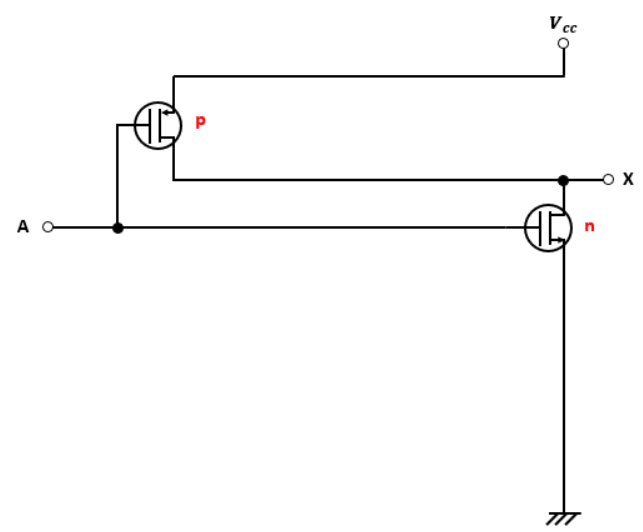
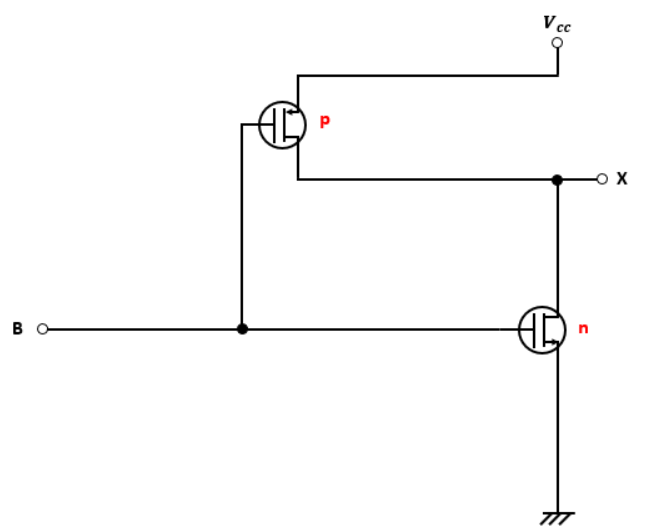
図3のように抜き出すと、ここもただのNOT回路だとわかります。
なので、出力XはBになります。
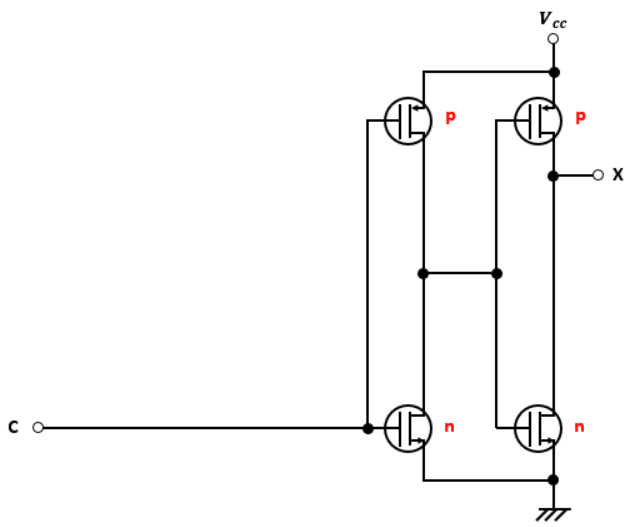
残りの回路は図4になります。
CをNOT回路で反転させ、その反転させた出力を他のNOT回路の入力としています。
つまり、出力XはCになります。
この3回路の出力が一箇所にまとめられているのが図1です。
なので、X=A・B・C…とすると間違いです。
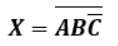
あくまで最終的にNAND回路としてまとめられるので勘違いしないようにしましょう。
この辺りはうまく言葉で説明ができる気がしません。
個人的には、CMOS論理回路のNAND回路の形状になっていたら、NOT回路の各入力に対してNAND出力とすると覚えています。
もしくは、図1を整理して図5のようにして考えていくのが良いと思います。
この形状になれば、AとBとCのNAND回路になっているのは一目瞭然なので混乱はせずに済みます。
3.例題②
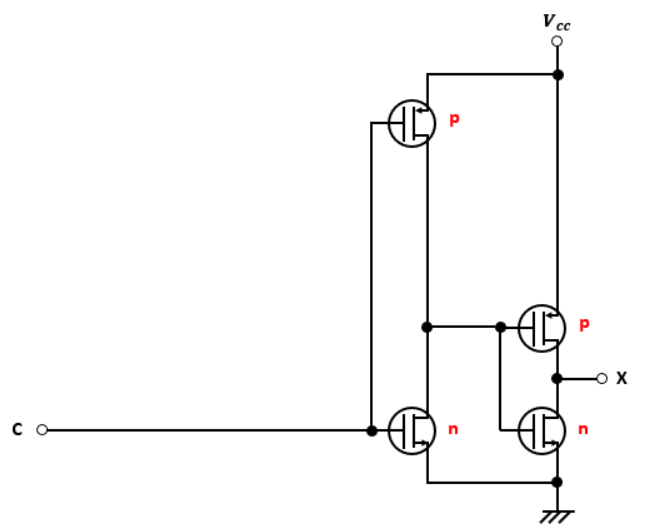
図6の論理式はどうなるか考えていきましょう。
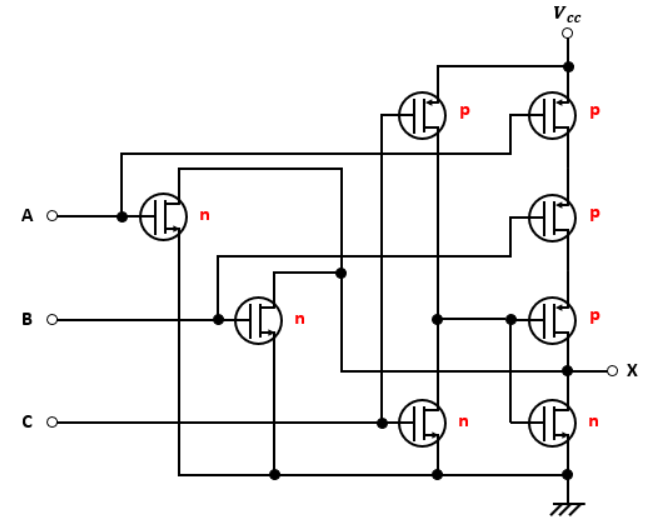
今度は一番右の列はn型MOSFETが1つに対してp型MOSFETが複数になっています。
なので、最終的にはNOR回路になっていることがわかります。
ということで、また分解して考えてみましょう。
まずは図7、図8のように抜き出してみました。
回路が遠回りしているだけで、これまたNOT回路なんですよね。
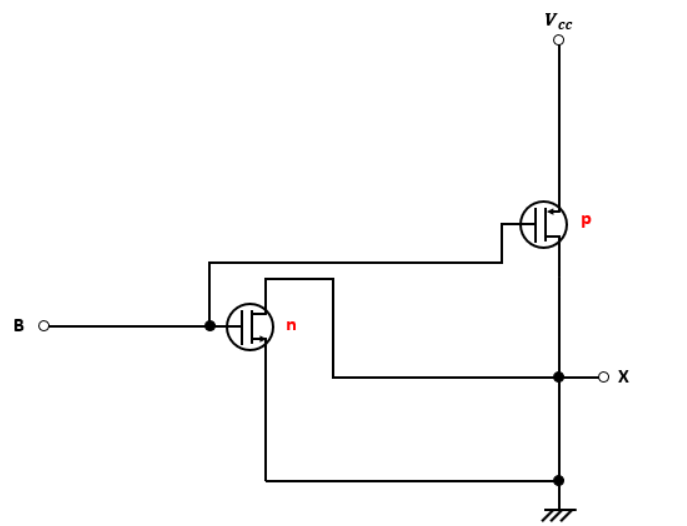
残りの回路は図9になります。
これまた先程と同じで、CをNOT回路で反転させ、その反転させた出力を他のNOT回路の入力としています。
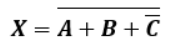
ややこしいですけど、こればかりは慣れてもらうしかないと思います。
以上、「CMOS論理回路の組み合わせ」についての説明でした。



