今回は、「論理ゲートのNAND・NOR・XOR回路」についての説明です。
1.ポイント
2つの入力に対して1つの出力があり、入力が両方“1”の時に出力が“0”になる回路。
Not AND回路。
2つの入力に対して1つの出力があり、入力のどちらか片方でも“1”になっていると出力が“0”になる回路。
Not OR回路。
2つの入力に対して1つの出力があり、入力がどちらか片方だけ“1”になっていると出力が“1”になる回路。
eXclusive OR回路。
EOR回路やEX-OR回路と呼ばれることもある。
2.論理ゲートとは?
論理ゲートとは、基本的な論理演算を行う電子回路のことです。
“0”と“1”の組み合わせから論理的な演算を行う回路が論理回路です。
「真理値表」の説明で述べましたが、2つの状態のことを真(1)または偽(0)と呼びます。
真は“1”、偽は“0”に対応させて表します。
これらの関係をダイオードやトランジスタなどの電子部品を使用した回路で実現し、“0”と“1”の2値の信号を“電圧0V”と“電圧3.3V”といった値で表現します。
この“電圧0V”と“電圧3.3V”を入力するための入力端子(ゲート)が設けられるので、論理ゲートと呼んでいるわけです。
ただ、特定の論理機能を実現する回路構成は1種類しかないわけではなく、様々な方法が存在します。
回路構成が違うのに論理機能は同じだとわかりづらいですよね?
その為、具体的な回路構成は省き、特定の論理機能を示す記号を用いて表現することが一般的です。
その特定の論理機能の中には基本論理と呼ばれている最も基礎的な論理機能があります。
その基本論理が論理積(AND)・論理和(OR)・否定(NOT)の3種類です。
基本論理の説明が必要な場合は先に以下の記事をご覧ください。

今回はNAND回路・NOR回路・XOR回路の説明をしていきます。
3.NAND回路とは?
NAND回路は否定論理積とも呼ばれています。
2つの入力に対して1つの出力があり、入力が両方“1”の時に出力が“0”になる回路です。
つまり、AND回路の結果が反転したものがNAND回路です。
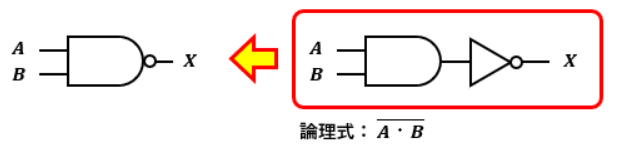
NAND回路の回路記号及び真理値表は以下の通りです。
| A | B | X |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
ANDの回路記号とNANDの回路記号を比較すると〇が付いているかどうかの差しかないですよね?
NOT回路の説明時にこの〇が反転の意味を持っていると述べました。
つまり、回路記号からもNAND回路はAND回路を反転させた結果となることが読み取れます。
そもそもNANDはNot ANDの略ですからね。
なので、AND回路にNOT回路を繋いだ構成になっているのがNAND回路と言えます。
次は実際の電気回路でイメージしてみましょう。
NAND回路のイメージはAND回路のイメージであるスイッチの直列回路にNOT回路がくっついたものとなります。
図1において出力Xに充分な電流が流れた時を“1”、スイッチAとスイッチBはそれぞれONの時に“1”だとします。
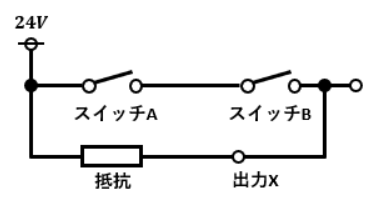
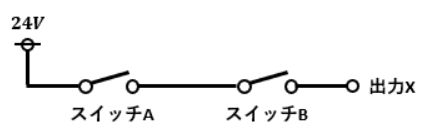
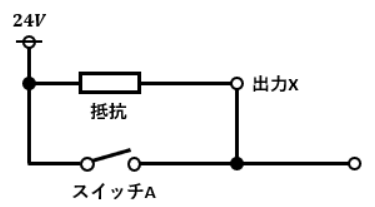
スイッチAとスイッチBが同時にONになると抵抗値の少ないスイッチ側に全電流が流れるので、出力Xに電流が流れなくなります。
逆に、スイッチAとスイッチBが同時にONになっている時以外は出力Xに全電流が流れます。
これがNAND回路のイメージです。
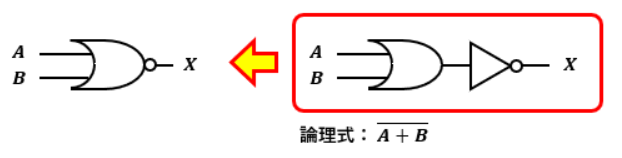
4.NOR回路とは?
NOR回路は否定論理和とも呼ばれています。
2つの入力に対して1つの出力があり、入力のどちらか片方でも“1”になっていると出力が“0”になる回路です。
つまり、OR回路の結果が反転したものがNOR回路です。
NOR回路の回路記号及び真理値表は以下の通りです。
| A | B | X |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
ANDの回路記号とNANDの回路記号の関係と同じく、ORの回路記号とNORの回路記号も〇が付いているかどうかの差しかないです。
NANDがNot ANDの略だったのと同じで、NORはNot ORの略でしかないのです。
なので、OR回路にNOT回路を繋いだ構成になっているのがNOR回路と言えます。
次は実際の電気回路でイメージしてみましょう。
NOR回路のイメージはOR回路のイメージであるスイッチの並列回路にNOT回路がくっついたものとなります。
図2において出力Xに充分な電流が流れた時を“1”、スイッチAとスイッチBはそれぞれONの時に“1”だとします。
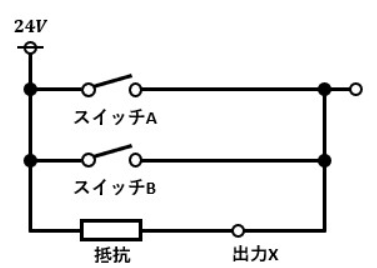
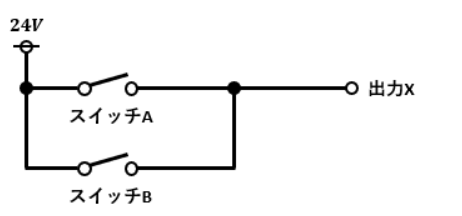

スイッチAとスイッチBのどちらか片方もしくは両方がONになると抵抗値の少ないスイッチ側に全電流が流れるので、出力Xに電流が流れなくなります。
逆に、スイッチAとスイッチBが同時にOFFになっている時は出力Xに全電流が流れます。
これがNOR回路のイメージです。
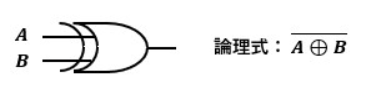
5.XOR回路とは?
XOR回路は排他的論理和とも呼ばれます。
媒体によってはXORではなくEORやEX-ORと表示されていることもあります。
XORはeXclusive ORの略で、「exclusive」の意味は「排他的」です。
「排他的」とは、「特定の主張だけを優遇する」という意味なので、“OR”だけを優遇するわけです。
“OR”は日本語だと“または”です。
つまり、2つの入力に対して1つの出力がある回路において、入力がどちらか片方だけ“1”になっていると出力が“1”になる回路を指しています。
あくまで“または”の状況を優遇するのであって“且つ(AND)”は“0”になる点には注意が必要です。
そこも“1”だとただのOR回路です。
XOR回路の回路記号及び真理値表は以下の通りです。
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR回路に関しても実際の電気回路に置き換えることは可能なのですが、NANDやNORと比べてごちゃごちゃしていて見ても混乱するだけなので割愛します。
ちなみに、何通りも組み方があって、複数のNAND回路を組み合わせたり複数のNOR回路を組み合わせたりして構成できます。
以上、「論理ゲートのNAND・NOR・XOR回路」についての説明でした。



