今回は、「論理ゲートのAND・OR・NOT回路」についての説明です。
1.ポイント
2つの入力に対して1つの出力があり、入力が両方“1”の時に出力が“1”になる回路。
2つの入力に対して1つの出力があり、入力のどちらか片方でも“1”になっていると出力が“1”になる回路。
1つの入力に対して1つの出力があり、出力は入力を反転させたものとなる回路。
“0”を入力すると“1”が出力され、“1”を入力すると“0”が出力される。
2.論理ゲートとは?
論理ゲートとは、基本的な論理演算を行う電子回路のことです。
“0”と“1”の組み合わせから論理的な演算を行う回路が論理回路です。
「真理値表」の説明で述べましたが、2つの状態のことを真(1)または偽(0)と呼びます。
真は“1”、偽は“0”に対応させて表します。
これらの関係をダイオードやトランジスタなどの電子部品を使用した回路で実現し、“0”と“1”の2値の信号を“電圧0V”と“電圧3.3V”といった値で表現します。
この“電圧0V”と“電圧3.3V”を入力するための入力端子(ゲート)が設けられるので、論理ゲートと呼んでいるわけです。
ただ、特定の論理機能を実現する回路構成は1種類しかないわけではなく、様々な方法が存在します。
回路構成が違うのに論理機能は同じだとわかりづらいですよね?
その為、具体的な回路構成は省き、特定の論理機能を示す記号を用いて表現することが一般的です。
その特定の論理機能の中には基本論理と呼ばれている最も基礎的な論理機能があります。
その基本論理が論理積(AND)・論理和(OR)・否定(NOT)の3種類です。
これまで散々説明してきた奴らですね。
論理積(AND)・論理和(OR)・否定(NOT)の元々の説明は以下の通りでした。
論理変数Aと論理変数Bの2つの状態が両方“1”の時に論理変数Xを“1”と出力する。
論理変数Aと論理変数Bの2つの状態がどちらか片方でも“1”の時に論理変数Xを“1”と出力する。
論理変数Aの状態が“0”の時に論理変数Xを“1”と出力し、論理変数Aの状態が“1”の時に論理変数Xを“0”と出力する。
入力の状態を反転して出力する。
考え方としては、この説明の論理変数がゲート(入力端子・出力端子)に置き換わるだけです。
詳しい説明は別個に行っていきますね。
3.AND回路とは?
AND回路は論理積とも呼ばれています。
2つの入力に対して1つの出力があり、入力が両方“1”の時に出力が“1”になる回路です。
AND回路の回路記号及び真理値表は以下の通りです。
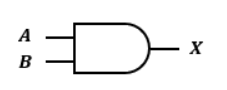
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
論理式はX=A・Bと書きます。
この書き方だとAとBを入力としたAND回路を表しているわけです。
実際の電気回路でイメージしてみましょう。
AND回路のイメージはスイッチの直列回路です。
図1において出力Xに24Vが供給された時を“1”、スイッチA及びスイッチBはそれぞれONの時に“1”だとします。
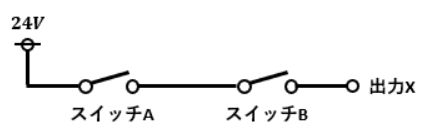
この回路において出力Xに24Vが供給されるのはスイッチAとスイッチBが両方ONした時のみですよね?
これがAND回路のイメージです。
4.OR回路とは?
OR回路は論理和とも呼ばれています。
2つの入力に対して1つの出力があり、入力のどちらか片方でも“1”になっていると出力が“1”になる回路です。
OR回路の回路記号及び真理値表は以下の通りです。
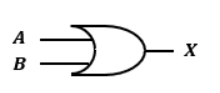
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
OR回路の回路記号は媒体によって微妙に異なる形状で記載されてることがあります。
入力端子側が丸みを帯びているという特徴は共通なので、そこで区別しましょう。
論理式はX=A+Bと書きます。
この書き方だとAとBを入力としたOR回路を表しているわけです。
実際の電気回路でイメージしてみましょう。
OR回路のイメージはスイッチの並列回路です。
図2において出力Xに24Vが供給された時を“1”、スイッチAとスイッチBはそれぞれONの時に“1”だとします。
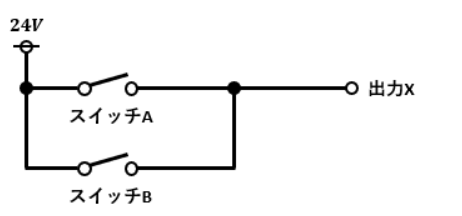
この回路において出力Xに起電力が供給されるのはスイッチAとスイッチBのどちらか片方もしくは両方がONになっている場合です。
逆に、出力Xに起電力が供給されないのはスイッチAとスイッチBが共にOFFになっている場合のみです。
これがOR回路のイメージです。
5.NOT回路とは?
NOT回路は反転回路と呼ばれています。
インバータとも呼ばれます。
AND回路とOR回路は入力が2つでしたが、NOT回路の場合は入力が1つになります。
出力は入力を反転させたものとなり、“0”入力すると“1”が出力され、“1”を入力すると“0”が出力されます。
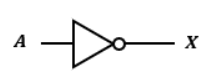
NOT回路の回路記号及び真理値表は以下の通りです。
| A | X |
|---|---|
| 0 | 1 |
| 1 | 0 |
論理式はX=Aと書きます。
回路記号の三角の横に〇が付いてますよね?
この〇が反転を意味しています。
実際の電気回路でイメージしてみましょう。
NOT回路のイメージはスイッチとの並列回路です。
図3において出力Xに充分な電流が流れた時を“1”、スイッチAはONの時に“1”だとします。
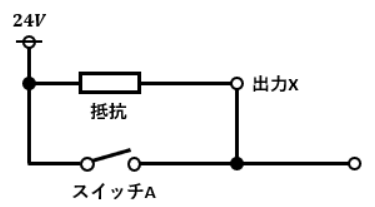
スイッチAがONになると抵抗値の少ないスイッチ側に全電流が流れるので、出力Xに電流がほぼ流れなくなります。
逆に、スイッチがOFFになっている時は出力Xに全電流が流れます。
これがNOT回路のイメージです。
論理回路はここで説明したAND回路・OR回路・NOT回路の組み合わせと言っても過言ではないので、しっかりと押さえておきましょう。
以上、「論理ゲートのAND・OR・NOT回路」についての説明でした。



