今回は、「電子放出と電界中・磁界中の電子の運動」についての説明です。
1.ポイント
通常、金属の表面付近には自由電子の脱出を妨げるエネルギーの壁(障壁)があるので、金属外部に電子が出ることはできない。
ただし、障壁の持つエネルギーを超えるエネルギーを外部から与えると自由電子は金属外部に出ることができる。
金属板間で電界が電子に与えたエネルギーは、電子が陽極に達した時点で保有している運動エネルギーと一致する。
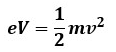
電子が磁界中で運動すると、ローレンツ力が働く。
ローレンツ力は常に電子の運動方向に対して垂直に働く為、電子は円運動をする。
ローレンツ力はフレミング左手の法則に則って向きを求めることができる。
ローレンツ力F[N]はF=Bevと表され、向心力との関係から以下の式が成り立つ。
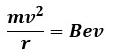
2.電子ボルトとは?
電子ボルト(エレクトロンボルト)とは、電子のエネルギーを取り扱う際の単位の1つです。
[eV]と表示します。
1個の電子が電位差V[V]の2点間で加速される時に電子に与えられるエネルギーW[J]はW=eVと表せます。
eは1個の電子が持つ電気量で、e≒1.602×10-19[C]です。(※電気素量と呼びます)
1個の電子が電位差1[V]の2点間で加速される時に電子に与えられるエネルギーW[J]はW=eと表せます。
この時のエネルギーを1[eV]と定義しています。
つまり、1[eV]≒1.602×10-19[J]です。
なんでわざわざ[eV]を使用するのかは調べてもよくわかりませんでした。
[J]で表すと10-19というとても小さな数字を扱う必要があるから、とかですかね?
ちなみに、W=eVの関係から、1[J]=1[CV]であることがわかります。
3.電子放出
電子は比較的自由に移動できます。
金属を構成する原子には多数の自由電子(束縛されていない自由に動ける電子)が存在します。
この自由電子の存在が熱や電気の伝導性に直結していると言われています。
通常、金属の表面付近には自由電子の脱出を妨げるエネルギーの壁(障壁と言う)があると考えます。
その為、金属外部に電子が出ることができません。
逆に言うと、障壁の持つエネルギーを超えるエネルギーを外部から与えると自由電子は金属外部に出ることができます。
この現象を電子放出と呼びます。
電子放出には色々種類がありますので、以下に例を記載します。
・熱電子放出
金属を熱して電子に熱エネルギーを与えることで電子を放出させる。
この時金属から放出された電子を熱電子と呼ぶ。
ちなみに、熱は振動で伝導するものなので、自由電子が無い物質も原子の振動により熱は伝わる。
自由電子を多く保有する物質は自由電子の振動も伝わるので、金属の多くは熱伝導性が高い。
・光電子放出
金属に光を照射して電子に光エネルギーを与えることで電子を放出させる。
この時金属から放出された電子を光電子と呼ぶ。
・二次電子放出
自由電子を金属に衝突させて電子に運動エネルギーを与えることで電子を放出させる。
この時照射した電子を一次電子、金属から放出された電子を二次電子と呼ぶ。
走査電子顕微鏡(SEM)なんかはこの仕組みを利用している。
・電界放出
電界を金属にかけて静電力により電子を放出させる。
4.電子の電界中での運動
ここまで、電位差のある2点間で電子を加速した時に電子に与えられるエネルギーと金属に充分なエネルギーを与えると電子が放出されることについて話をしてきました。
その内容を踏まえて、電子の電界中での運動について考えてみます。
図1のように金属板に電圧V[V]を加えているとします。
イメージとしてはコンデンサに直流電源を繋いでいる感じですね。
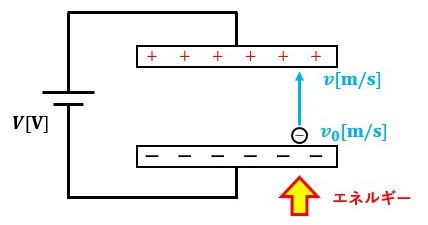
直流電源を接続したので、金属板にプラスとマイナスの電荷が蓄えられます。
この状態で陰極(マイナスに帯電している金属板)に外部からエネルギーを与えて電子放出を発生させます。
すると、金属板から放出された電子は陽極(プラスに帯電している金属板)に引かれて飛んでいきます。
電子が陰極から放出される際の初速度をv0[m/s]、陽極に辿り着いた際の速度をv[m/s]、1個の電子が持つ電気量をe[C]、1個の電子の質量をm[kg]とします。
ここでは、初速度はv0=0[m/s]とします。
金属板間で電界が電子に与えたエネルギーは、電子が陽極に達した時点で電子が保有している運動エネルギーと一致します。
1個の電子が電位差V[V]の2点間で加速される時に電子に与えられるエネルギーW[J]はW=eVと表せるので、金属板間で電界が電子に与えたエネルギーはeVです。
電子が陽極に達した時点で保有している運動エネルギーはmv2/2です。
※ 高校物理の内容です。
その為、以下の関係が成り立ちます。
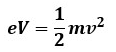
5.電子の磁界中での運動
電子(というより荷電粒子)が磁界中で運動すると、ローレンツ力が働きます。
ローレンツ力は常に電子の運動方向に対して垂直に働く為、電子は円運動をします。
ローレンツ力はフレミング左手の法則に則って向きを求めることができます。

フレミング左手の法則は、人差し指を導体の磁束の方向、中指を電流の方向に合わせると、親指が電磁力の発生する方向を示すという関係でした。
『磁束・電流・電磁力の向き…運動の向きは??』というのが私が最初に思った感想でした。
電流の向きを指す方向が電子の運動の方向に変わると考えて下さい。
電子の流れ=電流の流れ(逆方向)であるという関係から、電子の運動方向を電流の向きに合わせているのだと思います。
厳密には、荷電粒子(正電荷)に働くローレンツ力の向きはフレミング左手の法則に則って求めることができます。
その為、荷電粒子(負電荷)に働くローレンツ力の向きは運動の方向を逆向きに考える必要があります。
つまり、平等磁界中で電子が運動すると以下のように点Oを基準にした円運動の軌道を描きます。
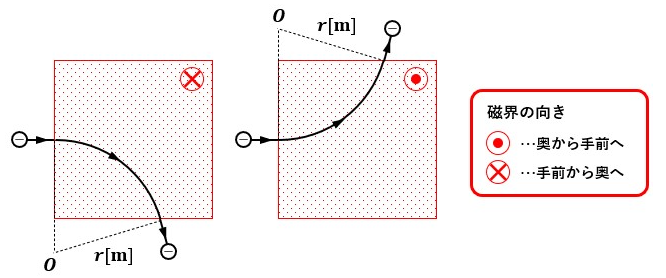
質量m[kg]、速度v[m/s]の物体(ここでは電子)が半径r[m]の円運動をする時の向心力(円運動の中心方向に働く力)の大きさF[N]は、F=mv2/rとなります。
磁束密度B[T]の平等磁界中を電気量e[C]の電子が速度v[m/s]で運動する際のローレンツ力F[N]は、F=Bevと表せます。
その為、以下の関係が成り立ちます。
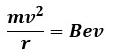
以上、「電子放出と電界中・磁界中の電子の運動」についての説明でした。



