今回は、「三平方の定理」についての説明です。
1.三平方の定理とは?
三平方の定理はピタゴラスの定理、勾股弦の定理とも呼びます。
この定理は、直角三角形の3つの辺の長さの関係を表しています。
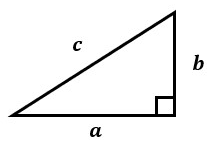
上図の直角三角形では、直角を挟む2つの辺の長さがa、bで、斜辺の長さがcとなっています。
この時、以下の式が成り立ちます。
a2+b2=c2
これが三平方の定理です。
この定理を知っていると、直角三角形を構成する辺のうち2辺の長さがわかっていれば残りの1辺の長さが算出できるようになります。
2.例題
定理を見ただけでは記憶に残りづらいので、実際に使ってみましょう。

直角三角形の辺a=4、辺b=3の時の辺cの値を求めましょう。
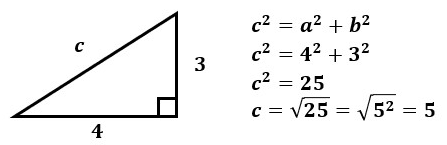
以上より、辺c=5であることがわかります。
√や2乗の説明が必要な場合は以下の記事を参考にしてください。

3.覚えておくと便利なこと
よく使われる直角三角形がいくつかあります。
特定の角度だと辺の比がそこそこスッキリすることがあるんです。
また、角度は微妙だけど辺の比がピッタリした数になることもあります。
特に、角度がわかる2つの直角三角形は覚えておくと便利です。
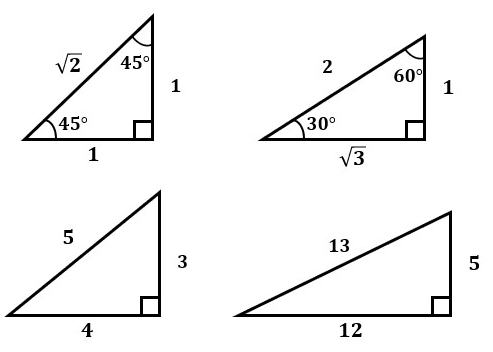
4.定理の証明
定理の証明方法は多くあるようですが、ここでは1つだけ記載します。
下図のように底辺a、高さbの直角三角形を4つ使用して、1辺の長さがa+bの正方形を作ります。
その際、内側にできた正方形の1辺の長さをcとします。
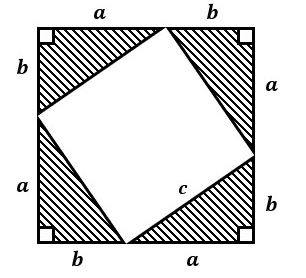
この図からわかる通り、「1辺の長さがa+bの正方形の面積」と「直角三角形4つの面積と内側の1辺の長さがcの正方形の面積を足し合わせた面積」は等しいです。
「1辺の長さがa+bの正方形の面積」は、(a+b)×(a+b)=a2+2ab+b2です。
「直角三角形4つの面積と内側の1辺の長さがcの正方形の面積を足し合わせた面積」は、(a×b)÷2×4+c2=2ab+c2です。
以上より、a2+2ab+b2=2ab+c2が成り立ちます。
2abを移項すると、a2+b2=c2となり、三平方の定理が証明できました。
5.おまけ
三平方の定理というと、私の頭にはある曲が思い浮かびます。
「SIREN:New Translation」というゲームの「恋の三角海域SOS」です。
「SIREN」はどのシリーズもよくできたゲームで、本編も面白いのですがおまけ要素に対しても謎の力を入れてくるんですよね。
一度聞くと頭にこびりついてくるので注意して下さい(笑)
ちなみに、三平方の定理はピタゴラスの定理とも呼びますが、ピタゴラスさんが発見したかどうかは定かではないらしいです。
以上、「三平方の定理」についての説明でした。



