今回は、「相対値と絶対値の違い」についての説明です。
1.初めに
相対的・絶対的という用語を聞いたことがありますか?
「相対的」はあまり聞き慣れないかもしれませんが、「絶対的」に関しては数学で「絶対値」を習うはずなので聞いたことがある方は多いでしょう。
…算数の時点で習ったっけ?
今回は、そんな相対値と絶対値の違いについて解説していこうと思います。
2.相対値とは?
相対値とは、基準から見た差のことです。
ベクトル量というヤツです。
例えば、室温20℃の部屋にいたとして、外は35℃になっていたとします。
暑いですね。
この時の温度差は、室内温度を基準とすると+15℃ですよね。
次に、室温20℃の部屋にいたとして、外は5℃になっていたとします。
寒いですね。
この時の温度差は、室内温度を基準とすると-15℃ですよね。
これらは、室温という基準から見た場合の外気温の差を表しています。
このような値が相対値に当たります。
3.絶対値とは?
絶対値とは、符号を考えない量のことです。
言い回しを変えると、基準点との量の差です。
スカラー量というヤツです。
先程の室温の例では、何れにしても『室温と比べると15℃違う』という点は同じでしたよね?
この、ある基準点(室温)との差(15℃)が絶対値です。
要するに、符号が常に正である変化量を指しているわけです。
絶対値の記号は「||」です。
この縦棒の中にある数値を強制的に正にします。
例)|+10|=10、|-10|=10
絶対値という名称自体はなんか難しそうですが、本質はなんてことないんですよね。
ちなみに、数学の世界では基準=0とされているので、絶対値について調べると「0との差」のように記述されている場合が多いです。
4.相対値と絶対値の違い
相対値と絶対値の違いは何となく理解してくれたかとは思います。
どこを基準にするか、符号が付くかという違いです。
ここでは、イメージを定着させるためにもう一つ、速度を例に解説していきます。
AさんとBさんが互いに直線上で向き合って点Pに向かって一定速度で歩いているとします。
数学とか物理って点O・点P・点Rがよく登場するよね。
Aさんの歩く速度は1[m/s]、Bさんの歩く速度は2[m/s]とします。
[m/s]というのは1秒間に何m進むかを表しています。
『2[m/s]なら1秒当たりに2m進みますよ~』ということです。
この時、Aさんから見たBさんの速度は1[m/s]+2[m/s]なので3[m/s]に見えます。
『何で?』と思う人向けに一応解説です。
1秒経過するとAさんは1m進んでBさんは2m進みますよね?
ということは、1秒で2人は3m近づいたわけです。
この繰り返しでお互いに1秒間に3mずつ近づいていく為、Aさんから見たBさんは3[m/s]で近づいてきているように見えますし、Bさんから見たAさんも3[m/s]で近づいてきているように見えます。
並走している車が遅く見えて、対向車線の車が異様に速くみえる現象がこれですね。
このイメージが相対速度です。
では、絶対速度はどうなのかというと、点Pのような動かない点が基準となります。
点Pから見たAさんは常に1[m/s]、Bさんは2[m/s]で移動しているように見えます。
点Pが動いていないということは、AさんとBさんが進む速度を変えない限りは絶対に速度が変わることがないです。
だから絶対速度です。
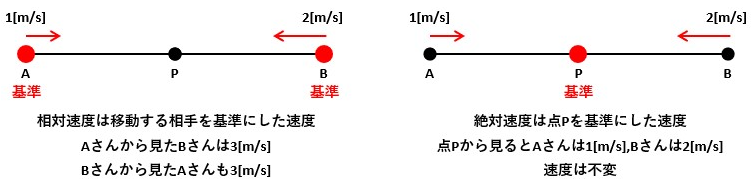
これが相対と絶対のイメージです。
以上、「相対値と絶対値の違い」についての説明でした。



