今回は、「真偽と真理値表」についての説明です。
1.ポイント
2つの状態を基にする論理体系のことを2値論理またはブール代数と呼び、2つの状態のことを真(true)または偽(false)と呼ぶ。
真は“1”、偽は“0”に対応させて表す。
論理式の論理変数の全組み合わせを網羅した表のこと。
2.2値論理と真偽
“0”と“1”の組み合わせから論理的な演算を行う回路が論理回路です。
「論理的演算に関する説明」で、スイッチがOFFの時に“0”、ONの時に“1”になるという具合に論理演算をするために2つの状態を定義していました。
このように、2つの状態を基にする論理体系のことを2値論理またはブール代数と呼び、2つの状態のことを真(true)または偽(false)と呼びます。
真は“1”、偽は“0”に対応させて表します。
“0”と“1”しか関係してこないので、数体系における2進数に対応しています。
| 真(true)(1) | 偽(false)(0) |
|---|---|
| スイッチON | スイッチOFF |
| 電圧あり | 電圧無し |
| 電流あり | 電流無し |
| センサ反応あり | センサ反応無し |
論理関係を表すためにはA・B・X・Yなどの記号を用います。
この記号のことを論理変数またはブール変数と呼びます。
スイッチAを論理変数A、スイッチBを論理変数Bと置き、それらの真偽(スイッチA及びスイッチBのON/OFFの状態)の組み合わせによって論理変数Xという結果を演算していくイメージです。
3.基本的な論理演算と論理式
論理演算には論理積(AND)・論理和(OR)・否定(NOT)という3種類の基本論理があります。
それぞれどういったものかを簡単にまとめると以下のようになります。
論理変数Aと論理変数Bの2つの状態が両方“1”の時に論理変数Xを“1”と出力する。
論理変数Aと論理変数Bの2つの状態がどちらか片方でも“1”の時に論理変数Xを“1”と出力する。
論理変数Aの状態が“0”の時に論理変数Xを“1”と出力し、論理変数Aの状態が“1”の時に論理変数Xを“0”と出力する。
入力の状態を反転して出力する。
論理積(AND)・論理和(OR)・否定(NOT)は以下のような記号で表されます。
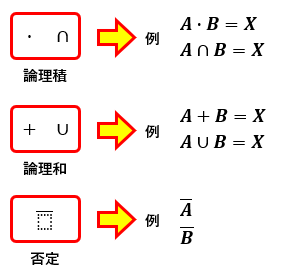
このようないくつかの論理変数と論理記号を用いた論理演算の関係式のことを、論理関数またはブール関数と呼びます。
論理式やブール代数式とも呼びます。
例えば、A・B=Xという論理式があった場合、論理変数Aと論理変数Bの論理和(AND)なので、AとBの両方が真(1)の時に論理変数Xが真(1)になることを示しているわけです。
4.真理値表とは?
A・B=Xという論理式があります。
この論理式は論理変数Aと論理変数Bの2つの状態が両方“1”の時に論理変数Xを“1”と出力するわけですが、Aが“0”でBが“1”の時はXは“0”になるという具合に論理変数の他の組み合わせも存在します。
この論理変数の全組み合わせを網羅した表を真理値表と呼びます。
A・B=Xを例にすると、真理値表は以下のようになります。
| A | B | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
A・B=Xのような簡単な論理式の場合は真理値表にあまり必要性を感じませんが、もっと複雑になってくると視覚的にわかりやすくて便利に感じてきます。
以上、「真偽と真理値表」についての説明でした。




